প্রাথমিক গণিত-২ : পরশ পাথরের খোঁজে

রুবাই-এর পরীক্ষা চলে এসেছে। কাজে নানান বিষয়ে পড়তে হচ্ছে। ইচ্ছে হলেই এখন আর আমার সঙ্গে পড়তে বসতে পারে না। আর বিদুষীও ভাই-এর পেছনে সেভাবে লাগতে পারে না। বিদুষীর স্কুলে আবার শুরু হয়েছে গ্রীস্মকালীন এবং বাৎসরিক ছুটি। ওর অনেক মন খারাপ কারণ স্কুল যখন খুলবে তখন তাকে নতুন ক্লাশে যেতে হবে!

আমি ভাবলাম ও সারাদিন বাসায় থাকে ওকে বরং একটা বড় কাজ দেওয়া যাক। যেমন মৌলিক সংখ্যা খুঁজে বের করা। তোমাদের নিশ্চয়ই মনে আছে ২, ১১, ১৯, ২৩, ৫৩ এই সংখ্যাগুলো সংখ্যার জগতে অন্যরকম। কারণ এ সংখ্যাগুলোর মাত্র দুটি গুণনীয়ক অথবা বিভাজক রয়েছে। সে নিজে এবং ১! এর মানে হলো এ সংখ্যাগুলোকে অন্য কোনো সংখ্যা দ্বারা নিঃশেষে ভাগ করা যায় না।
এ ধরনের সংখ্যাকেই বলা হয় মৌলিক সংখ্যা। সংজ্ঞায়নের সুবিধার্থে ১ কে মৌলিক সংখ্যা হিসেবে ধরা হয় না। মৌলিক সংখ্যা ছাড়া বাকি সব সংখ্যাই যৌগিক সংখ্যা।
সেই অনেককাল আগে থেকে মানুষ মৌলিক সংখ্যা নিয়ে কাজ করেছে। জানতে চেয়েছে কোনটি মৌলিক সংখ্যা আর কোনটি নয়।
সেদিন বাসায় ফেরার পর বিদুষী জানালো তাঁর রিসার্চ শেষ। সে ফলাফল জানাতে চায়। তো আমরা বাপ-বেটি বসে পড়লাম আমাদের গণিতের আসরে।

বিদুষী জানালো – বাবা, তুমি তো জানো, কোনো একটি সংখ্যা মৌলিক সংখ্যা কি না, সেটা জানার সহজ বুদ্ধি হলো, ওই সংখ্যাকে ২ থেকে বড় কিন্তু ওই সংখ্যা থেকে ছোট সব মৌলিক সংখ্যা দিয়ে ভাগ করা।
বললাম – এটাতো আমরা সবাই জানি।
“হ্যা। তবে তবে কতক সোজা বুদ্ধি আছে।“ বিদুষী বলে-“ সংখ্যাটি যদি জোড় সংখ্যা হয়, তাহলে সেটি অবশ্য ২ দ্বারা বিভাজ্য হবে। অর্থাৎ ২ ছাড়া সব জোড় সংখ্যাই যৌগিক সংখ্যা। আর জোড় সংখ্যা চেনা তো সহজ। তাই না?

আমি দেখলাম তাইতো। কোন সংখ্যার শেষ অংকটা যদি হয় ০,২,৪,৬ বা ৮ তাহলে তো সেটি জোড় সংখ্যা। তার মানে দাড়ালো ১৪২, ১২৩৪৫৬৭৮, ৩০০০৩৯৮৬৫৪০ এই সংখ্যাগুলোর দিকে তাকিয়ে সহজে বলে দেওয়া যায় সেগুলো মৌলিক সংখ্যা নয়!
বিদুষী বেশ কিছু নতুন কথা আমাকে জানালো। জোড় সংখ্যার ব্যাপারটাতো শেষ। কিন্তু বেজোড় সংখ্যার বেলায়। ছোট সংখ্যা দিয়ে ভাগ করার ক্ষেত্রে আমাদের কত দিয়ে ভাগ করা উচিত, নিশ্চিত হওয়ার জন্য?
যদি একটি সংখ্যা যৌগিক সংখ্যা হয়, তাহলে সেটিকে একাধিক মৌলিক সংখ্যার গুণফল হিসেবে প্রকাশ করা যায়। যেমন ৬ = ২×৩, ১৫ = ৩×৫ ইত্যাদি।
যদি কোনো সংখ্যা মৌলিক না হয়, তবে তার কমপক্ষে দুটো মৌলিক উৎপাদক থাকবে।
অর্থাৎ সেই যৌগিক সংখ্যা N কে আমরা P1×P2 আকারে প্রকাশ করতে পারব।
আমি বললাম – হ্যা। এটাতো নতুন কিছু না।
বিদুষী বললো- ঠিক বাবা। নতুন কিছু না। কিন্তু একটু ঠান্ডা মাথায় ভাবো যদি P1=P2 হয় তাহলে কী হবে?
আমি বললাম – বাহ, এতো সহজ। তখন N হবে একটি বর্গ সংখ্যা এবং P1 হবে এর বর্গমূল।
“ঠিক ধরেছো, বাবা। এর মানে হলো N= P1×P2 হয় তাহলে P1 এবং P2-এর দুটি আলাদাভাবে N-এর বর্গমূলের চেয়ে বড় হতে পারবে না। পারবে?”
“না।” স্বীকার করাই ভাল।
“কাজেই, মৌলিকত্ব বের করার জন্য সব মৌলিক সংখ্যা দিয়ে ভাগ করার দরকার নেই।” বিদুষী খুশি। “কেবল ঐ সংখ্যার বর্গমূলের চেয়ে ছোট মৌলিক সংখ্যা দিয়ে ভাগ করলে চলবে। অর্থাৎ ৮১৭ মৌলিক সংখ্যা কিনা তা বের করার বুদ্ধি হলো, প্রথমে ৮১৭-এর বর্গমূল বের করা। তারপর ৮১৭ কে বর্গমূলের চেয়ে ছোট মৌলিক সংখ্যাগুলো (২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩) দিয়ে ভাগ করা। এ করলে দেখা যাবে, ৮১৭ আসলে মৌলিক সংখ্যা নয়।
যাক, বিদুষীর কল্যানে জনা গেল মৌলিক সংখ্যা চেনার জন্য ঐ সংখ্যা থেকে ছোট সব মৌলিক সংখ্যা দিয়ে ভাগ করার দরকার নাই। বললাম – তোমার ভাই-এর পরীক্ষা শেষ হলে তাকে একটি
কম্পিউটারে প্রোগ্রাম লিখতে বলো যা কিনা সহজে একটি সংখ্যা মৌলিক কিনা বের করে দেবে।
[ যারা এই লেখা পড়ছো, তোমরা এই ফাকে হাতে-কলমে কিছু মৌলিক সংখ্যা বের করার চেষ্টা করব। নিচের সংখ্যাগুলোর কোনটি মৌলিক?
২৭, ৫১, ৭৩, ১৩৩, ১৮৭, ১৯৭, ২২৯, ২৫০]

মৌলিক সংখ্যার ছক

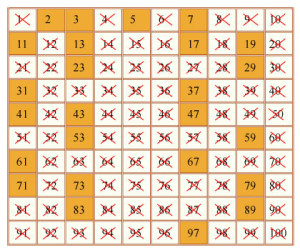বিদুষী বললো, “বাবা আগে তো কম্পিউটার ছিল না। ওরা কেমনে বের করতো?” আমি অনেকগুলো খুজে পেয়েছি। মৌলিক সংখ্যা খোঁজার চেষ্টা যুগ যুগ ধরে গণিতবিদেরা করছেন। এর মধ্যে একটি মজার পদ্ধতি হলো, গ্রিক গণিতবিদ ইরাতোসটিনের ছক। ইরাতোসটিন খ্রিষ্টের জন্মের ২৭৫ থেকে ১৯৫ বছর আগে কর্মক্ষম ছিলেন। তার ছক থেকেও মৌলিক সংখ্যা বের করা যায়।
আমি বললাম – এটা যদি অনেক বড় বানাই তাহরে তো কাটতে কাটতে আমরা হাত ব্যাথা হয়ে যাবে? কোন সহজ বুদ্ধি নাই?
বিদুষী বললা – তুমি কী মৌলিক সংখ্যার কোন সূত্রের কথা বলছো? চলো দেখি সেরকম কিছু পাওয়া যায় কী না।
প্রথমে ধারণা ছিল নিচের সূত্রে থেকে মৌলিক সংখ্যা বের করা যায়। সূত্রটি হল-

N = n*2-n+41

এই সূত্রে n-এর মান ১ থেকে ৫০ পর্যন্ত বসিয়ে নতুন সংখ্যা বের করে আগের নিয়মে দেখা যায় সংখ্যাটি মৌলিক কি না।
ঠিকমতো হিসাব করলে দেখবে, ১ থেকে ৪০ পর্যন্ত মৌলিক সংখ্যা পাওয়া যাচ্ছে। তারপরই লাগবে ফ্যাসাদ।
একইভাবে —
(N) = n*2-79n+1601

এই সূত্র n=১ থেকে ৭৯ পর্যন্ত মৌলিক সংখ্যা বের করতে পারে।

ফরাসী আইনজীবী-গণিতবিদ পিয়েরে দ্য ফার্মা (১৬০১-১৬৬৫) তাঁর শেষ উপপাদ্যের জন্য জগদ্বিখ্যাত। তিনি মৌলিক সংখ্যার জন্য একটি সূত্র প্রকাশ করেন। তাঁর সময়ে কোনো ক্যালকুলেটর ছিল না। এই সূত্রের সংখ্যাকে বলা হয় ফার্মার সংখ্যা।

তার সূত্রটি ছিল

2*2*n+1
n-এর যে কোন মানের জন্য মৌলিক সংখ্যা হবে। প্রথম পাচটি ফার্মা সংখ্যা হল-
F০ = ৩
F১ = ৫
F২ = ১৭
F৩ = ২৫৭
F৪ = ৬৫৫৩৭ যে মৌলিক তা জানা যায়। তখন অনেকেই তাঁর এই সূত্র মেনে নেন।

তবে, তাঁর মৃত্যুর শ খানেক বছর পর গণিতবিদ লিওনার্দো অয়েলায় প্রমাণ করেন, F৫ যৌগিক, মৌলিক নয়!
ফার্মার সংখ্যাগুলো খুবই বিশাল। এগুলোকে উৎপাদকে বিশ্লেষণ করা চাট্টিখানি কথা নয়। F১৭ যে যৌগিক, এটা প্রমাণ হয়েছে ১৯৭০ সালে। আর দেখো, F৭ এর উৎপাদক
F৭ = ৫৯,৬৪৯,৫৮৯,১২৭,৪৯৭,২১৭×৫,৭০৪, ৬৮৯,২০০,৬৮৫,১২৯,০৫৪,৭২১

বিদুষীর গবেষণার ফলাফলে আমি মোটামুটি হয়রান হয়ে পড়েছি। তাড়াতাড়ি জানতে চাইলাম – আচ্ছা মৌলিক সংখ্যা খোঁজা বাদ দেই। তবে শেষ প্রশ্ন মৌলিক সংখ্যার কি শেষ আছে?

হাসতে হাসকে বিদুষী জানালো – না, নেই। শেষ যে নেই, তার একটি সুন্দর প্রমাণ দিয়েছেন ইউক্লিড। সেটা কি এখন বলবো।

আমি বললাম – না, সেটা থাক। পড়ুয়া বন্ধুরা বরং সেটা নিজেরাই খুঁজে নিক।