ত্রিভূজ খোঁজার আনন্দ

দিন দুই আগে আমার ফেসবুক প্রোফাইলে একটি পুরানো জ্যামিতিক প্রবলেম দিয়েছিলাম। তেমন কোন উদ্দেশ্য ছিল না। পরদিন দেখলাম অনেকেই ধাঁধাটি সমাধান করেছেন। গুনে দেখলাম ৫০% সঠিক সমাধান করেছেন। বাকীদেরটা ভুল।

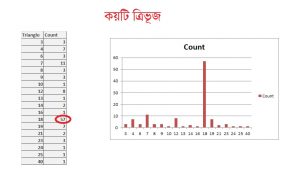
সমাধানের একটা চার্টও বানালাম। দেখলাম একজন ৪০টি ত্রিভূজ খুঁজে পেয়েছেন!

সমাধান পড়ে অনেকের চিন্তার সূত্র ধরতে চাইলাম। মানে আসলে এমন একটা সমস্যার কীভাবে সমাধান করে?

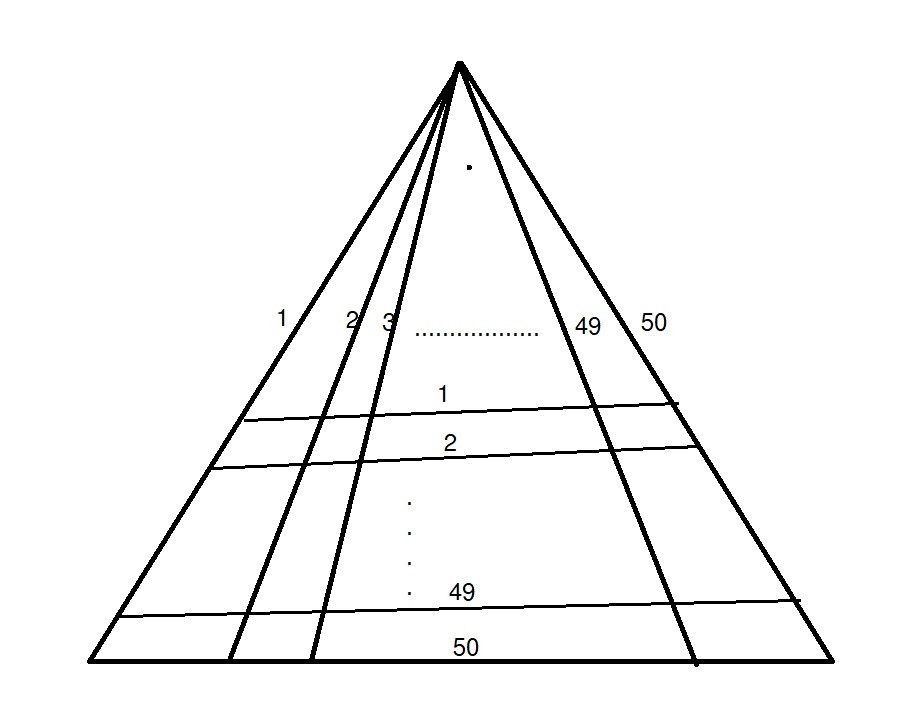
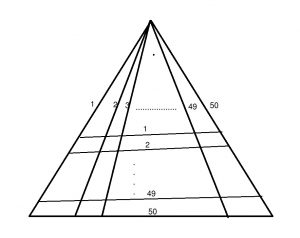
ফেসবুকের বাইরে কয়েকজনকে এটা করতে দিলাম। অনেকেই সহজ রাস্তা ধরেন, ব্রুট ফোর্স। গুণে ফেলা। একজনকে ঠেকানোর জন্য নিচের ছবি একে দিলাম।

উপরের ছবিতে ভূমির সমান্তরাল রেখার সংখ্যা ৫০ আর শীর্ষবিন্দুগামী রেখার সংখ্যাও ৫০! এর মানে হলো গুণে গুণে এই সমস্যার সমাধান করা যাবে না। ছবি দেখে উনি বললেন -আপনার পাগলামি আপনি করেন। আমার ওতো সময় নাই।

আমি অবশ্য ভেবেছি একটি হাইস্কুল পড়ুয়া শিক্ষার্থীকে এই ধরণের সমস্যা সমাধানে কেমন করে প্রক্রিয়াগত চিন্তা করানো যায়। সেই চিন্তা থেকে একটা প্রক্রিয়া অনুসরণের চেষ্টা করলাম।
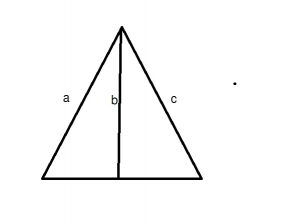
প্রথমত একটা ত্রিভূজ মানে হলো – ভূমি আর ভূমি সংলগ্ন দুইটি রেখার শীর্ষ বিন্দু দিয়ে যাওয়া। এরকম হলে আমরা একটি মাত্র ত্রিভূজ পাবো। এখন আমি যদি শীর্ষবিন্দুগামী রেখার সংখ্যা দুই এর বদলে তিনটা করি তাহলে আমার কয়টা ত্রিভূজ হবে? সোজা। তিনটা। গুণেই পাওয়া যায়। তবে, এটি অন্যভাবেও আমরা ভাবতে পারি। এই ক্ষেত্রে আমাকে ভূমি সংলগ্ন তিনটি রেখা থেকে প্রতিবার দুইটি করে রেখা নিতে হবে। সেরকম রেখা আমারা কতোভাবে নিতে পারি –

রেখা তিনটি যদি হয় যথাক্রমে a, b আর c। তাহলে আমাদের অপশন হচ্ছে – a ও b, a ও c এবং  b ও  c। তিনটেই। দাঁড়ান!

হাইস্কুলে এটা পড়েছি আমরা তাই না। এ হলো তিনটে বস্তু থেকে যে কোন দুইটা বস্তু খুজে নেওয়ার বুদ্ধি। এন সি আর!!! বা n choose 2। এটা হলো n(n-1)/2!!!

তাহলে আমরা কিন্তু একটা অংশের সমাধান করে ফেলেছি। আমাদের জানতে হবে ভূমি সংলগ্ন কয়টা রেখা আছে (n)। ব্যাস জানা হয়ে গেল। আমাদের মূল সমস্যায় রেখার সংখ্যা ৪। তার মানে এখানে কম্বিনেশন হবে ৪(৪-১)/২==৬!!!

এরপর দেখা যাক, ভূমির সমান্তরাল সরলরেখাগুলোর ভূমিকা কী। এটির জন্য ছবির দিকে তাকালেই বোঝা যায়। এগুলো কেবল ত্রিভূজের সংখ্যাকে গুণিতকে বাড়িয়ে যায়। ভূমির সমান্তরাল রেখা ২ মানে দ্বিগুণ, ৩ মানে তিনগুণ।

তাহলে আমাদের হিসাবটা কী হবে?
যদিভূমির সমান্তরাল রেখার সংখ্যা p আর ভূমি সংলগ্ন রেখার সংখ্যা n হয়, তাহলে আমাদের ত্রিভূজের সংখ্যা হবে p*n(n-1)/2!!!

ব্যাস হয়ে গেল। তারমানে আমাদের অরিজিনাল সমস্যার সমাধান হলো ৩*৪(৪-১)/২=১৮!!!
ভয়লা! হয়ে গেল।

এখন আমরা ভাবতে পারি হাইস্কুলের একটি বাচ্চাকে এই চিন্তাতে কীভাবে প্রভাবিত করা যায়। আমার ধারণা উত্তরটা আমরা এর মধ্যে পেয়ে গেছি?
তাঁকে ৫০ এর সমস্যায় ফেলে দিয়ে গাইড করা।  তাকে দেখানো উভয় দিকে রেখার সংখ্যা বাড়ানো হলে সেটার প্রভাব কীভাবে পড়ে।
অনেকেই বলতে পারেন, এর সি আরের ফর্মুলা তো ও জানে না। সেক্ষেত্রে তাকে ২, ৩ এবং ৪ পর্যন্ত দিয়ে সেখান থেকে দুইটি রেখা বাছাই-এর কাজটা ম্যানুয়ালি করতে দেওয়া যায় যাতে এন চুজ টু -এর বুদ্ধিটা সে বের করে ফেলতে পারে।
ভিয়েতনামসহ পূর্ব এশিয়ার দেশগুলো শিক্ষর্থীদের ৫ম শ্রেণী থেকে পারমুটেশন-কম্বিনেশনের এই কাজগুলো করতে দেয়, কোন ফর্মুলার প্রয়োগ না করে। বাচ্চারা বিভিন্ন উপকরণ সাজিয়ে এ কাজটা করে। তাতে ছোটবেলা থেকে বিন্যাস-সমাবেশের একটি ধারণা তার মধ্যে বিকশিত হয়।

সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক।