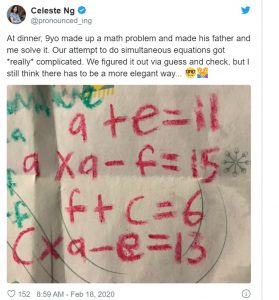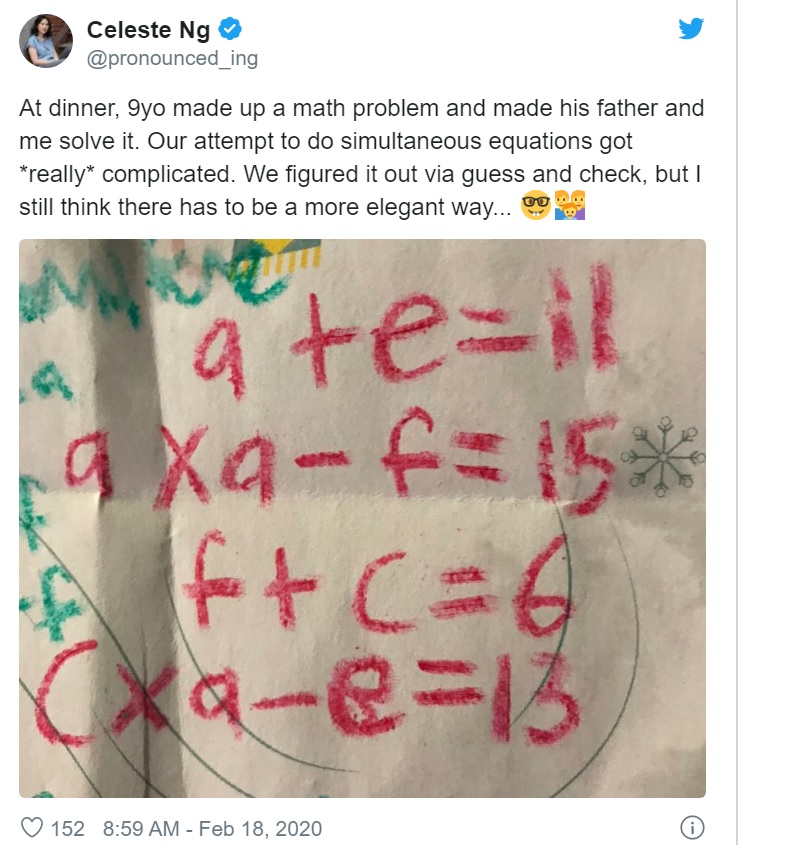
নেই খাজ তো খই ভাঁজ – ৯ বছরের শিশুর বানানো সমস্যা
আমেরিকান লেখক ও ঔপন্যাসিক সেলেস্টে নং(??,Celeste Ng) ফেব্রুয়ারির ১৮ তারিখে তার ৯ বছরের মেয়ের একটি গাণিতিক সমস্যা টুইটারে পোস্ট করেন। তিনি লিখেছেন সমস্যাটি ওনারা অনুমান আর ট্রায়াল দিয়ে সমাধান করেছেন। কিন্তু অন্যভাবেও হয়তো সমাধান করা যায়।
বাসায় থাকার সুবাদে সবাই সে সমস্যার সমাধানের চেষ্টাও করছেন। আজকে আমিও করলাম।
এখানে চারটি অজানা রাশি এবং চারটি সমীকরণ আছে। কাজে যারা সাধারণ বীজগণিত পারে তারা সেই নিয়মে এটি সমাধান করতে পারে। তবে অন্যভাবেও সমাধান করা যায়। সমীকরণগুলো দেখা যাক –
a+e=11 —(১)
a×a –f=15 ……(২)
f+c=6 ………(৩)
a×c –e=13 ……(৪)
ঝামেলা হলো দুই নম্বর সমীকরণটি। এটি একটি দ্বিঘাত সমীকরণ। কিন্তু এটা থেকে সমাধান করাটা সহজ –
a×a –f=15
=> a×a=15+f …………(৫)
আমরা যদি এই সমস্যার সমাধানগুলো পূর্ণ সংখ্যা বলে ধরে নেই (৯ বছরের একটি শিশু তো) তাহলে ৫ নং সমীকরণ থেকে a এর মান হতে পারে 4,5 বা 6 এর একটা কিছু হবে। ৩ ও ৪ নম্বর সমীকরণ থেকে টের পাচ্ছি f এর মান আসলে অনেক কম হওয়া দরকার। সেক্ষেত্রে a এর মান হবে 4। তাহলে f হবে 1। বাকী সমাধান গুলো সহজে করা যায়।
শেষ পর্যন্ত {a,c,e,f} = {4, 5, 7, 1}
যারা এলিমিনেশনে চেষ্টা করছেন তারা মিলিয়ে নিতে পারেন।
হ্যাপি প্রবলেম সলভিং